
Tíhové anomálie
Při zpracování měření měření je nutné zahrnout negeologické vlivy okolního prostředí. Patří sem vlivy způsobené Sluncem a Měsícem, odstředivé zrychlení, nadmořská výška měřeného bodu a reliéf terénu. Při těchto operacích je nutné vzít v potaz i chod přístroje, tzn. subtilní změny citlivosti přístroje.
Závislost na zeměpisné šířce (odstředivém zrychlení) odstraníme odečtením normální tíže gn od naměřené tíže g. Hodnota gn se vypočítá dle vzorce:
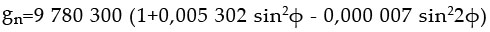
kde φ je zeměpisná šířka.
Odstranění vlivu nadmořské výšky je poměrně složité. Má-li bod nulovou nadmořskou výšku, nemusíme tuto opravu zavádět. Je-li bod měření v určité nadmořské výšce, je nutno ho převést na nulovou nadmořskou výšku. Tzn. k naměřené tíži se přičte Fayova oprava a odečte se od ní oprava z Bouguerovy desky. Oprava na nerovnosti terénu se nazývá topografická korekce a je vždy kladná.
Principem Fayovy opravy je odstranění tíhového vlivu rotujícího elipsoidu. Fayovy opravy lze také najít pod názvem anomálie z volného vzduchu (anglicky Free-air anomalies), protože při přenesení teoretické tíže z hladiny elipsoidu do bodu měření se mění gravitace s výškou. Fayovu opravu vypočítáme přes vzorec:
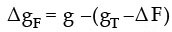
kde g je měřená tíže, gT teoretická tíže na hladině elipsoidu - funkcí zeměpisné šířky φ, a ΔF je fayova korekce, která je funkcí nadmořské výšky h.
Bouguerova anomálie zahrnuje Fayovu opravu a navíc je v ní odstraněn účinek všech „normálních“ hmot nad hladinou moře (referenčního elipsoidu) a vliv reliéfu terénu. Bouguerovu anomálii spočítáme:
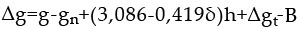
kde g je naměřená tíže, gn normální tíže, 3,086h Fayova oprava, -0419δh je oprava z Bouguerovy desky, ∆gt je terénní korekce a B Bullardův člen. Ten kompenzuje skutečnost, že při přesných výpočtech je nutné Bouguerovu desku ohraničit kulovými plochami.
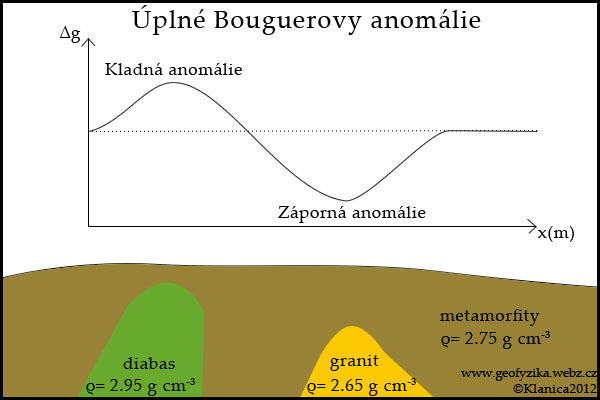
Modelový vliv těles o různé hustotě pod povrchem země na Bouguerovu anomálii. Osa Y ukazuje hodnotu Bouguerovy anomálie ∆g, osa X reprezentuje vzdálenost v metrech.
Na konec již zbývají jen izostatické anomálie. Ty dostaneme tak, že k úplným Bouguerovým anomáliím přičteme izostatickou korekci. Pokud jsou izostatické anomálie nulové, je zkoumaný celek izostaticky kompenzovaný. Pokud jsou kladné (záporné), je celek nedokompenzovaný (překompenzovaný), to znamená, že kořeny hor jsou málo (příliš) hluboké. Na izostatické anomálie existuje několik teorií. Airyho předpokládá lokální kompenzaci: kořenová zóna hory leží přímo pod ní. Prattova naopak předpokládá, že hydrostatické rovnováhy v hloubce CC’ je dosaženo tím, že bloky zemské kůry mají různou hustotu: čím vyšší blok, tím nižší hustota. Meineszova přepokládá vyšší elasticitu svrchních vrstev Země a předkládá hypotézu regionální izostatické kompenzace.


